The minimalist program
is an effort to discover the degree to which the human language faculty is
determined by sensorimotor and conceptual-intentional “interface condition”
together with consideration of visual necessity in particular by general
considerations of simplicity elegance and economy Langendoen (2001). It was
developed by Noam A. Chomsky and his followers since 1990s. It aims to
eliminate from linguistic theory anything which is not “virtually necessary”.
For instance Chomsky claims that D-structure and S-structure can be dispersed
with. The minimalist program deals with the perennial question of law to link
sound and meaning.
It works on the
assumption that universal grammar constitutes a perfect design in the sense
that it contains only what is necessary to meet our conceptual and physical
(phonological) needs.
The minimalist program aims at farther
development of ideas involving economy of representation. Economy of deviation
is the principle stating that movements (that is transformation) only occur in
order to match interpretable features with uninterpretable features. An example
of an interpretable feature is plural
inflection in regular English nouns like dogs, pens. The word dogs can only be used to refer to several dogs
and not a single dog, and so this inflection contributes to meaning making it
interpretable. English verbs are inflected according to the number of their
subject (example: dogs bite versus a dog bites) but this information is
only interpretable once a relationship is formed between the subject and the
verb, therefore movement of the subject is required.
The notion of economy of derivation
applied is a global one which entails
that various derivations are compared and the most economical one is selected
as the only one allowed. In some cases where two derivations are equally
economical, we get optional word order variation (as in French souvent paraître triste and paraître souvent triste). Chomsky however, notes that economy cannot simply reduce to the matter of counting
steps, such a do-insertion, a more
costly than universal ones, a notion substantially move more costly than merge
(Zwart, 1998).
D-structure is eliminated in the sense
that there is no base component applying rewrite rules to generate an empty
structure which is to be flashed out that by “all at once” lexical insertion.
Instead structures are created by combining elements drawn from the lexicon and
there is no stage in the process at which we can stop and say: this is D-structure.
The approach leads to a unification of insertion (merge) and movement which
differs from merge only in that the element to be merged is contained in the
target.
Differences between languages at S-structure
are reduced to requirements at the PF interface. Certain features that are
visible but not interpretable at PF must be eliminated by the feature checking
operation (a function of movement). Hence, there is no need for language
particular S-structure conditions in order to describe word order variation.
Chomsky assumes that language is a
system whose “generative engine” which is narrow syntax, constructs a
derivation for each choice of lexical array. He asserts that narrow syntax has
one operation that comes free in that, it is required in some form for any
recursive system – the operation merge. The condition that language is
recursive system is imposed by the conceptual-intentional interface. Merge is
therefore ‘free’ a consequence of general principles, because recursion is
impossible without it.
A major concern of the minimalist program is to be remembered as the reduction of the computational load in
carrying out a derivation. A natural extension of that concern is the reduction
of the complexity of the generated objects themselves, such as their degree of
embedding, without sacrificing expressive power (Langendoen, 2001).
Merge is, therefore, basically said to
be not a single operation but a family of operations. An operation must be able
to yield an infinite set of objects from a finite basis for it to become to the
merge family. What type of merge operations are appropriate for narrow syntax
depends on the nature of the infinite set of objects it is required to create.
In a set merge, Chomsky identifies the
simplest form that merge can take as the formation of two-member sets.
Applied to two objects, α and β, merge forms the
new object “ϒ”. In this, Langendoen (2001)
puts that, “ϒ” must be constituted
somehow from the two items α
and β. The simplest form
constructed from α and β is the set {α, β}, so we take “ϒ” to
be at least this set. Merge takes two elements α, β already constructed and creates a new one consisting of the two
- in the simplest case {α, β}.
Chomsky calls merge the “set merge”. Further; set merge is “external” α
if, and β are separated objects, and internal (essentially ‘move’) if one
is the part of the other. For instance, if β is part of α, in which case β is said
to be a ‘copy’ of its occurrence in α , he contends that, external set
merge builds ‘argument structure’ where as internal set merge builds the
structure required for “scopal and discourse related properties”.
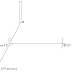
Langendoen (2001)
shows the result of externally merging c with the result of externally
merging a and b. S(S (a, b), c) = {{a, b}, c}; the
objects a, b, and c are not necessarily atomic
(lexical). The derivation can also be diagrammed as a tree in the following
figure, where the root and internal node labels are sets, not categories. Since
the relation S is symmetric, the
order of nodes in the tree is not significant. (The operator S is commutative).
However, Chomsky
solves the problem pointed by other linguists as inadequacy of his set merge.
They say when the object α and β are merged, one of them is the head. But the result of their set
does not indicate which one, since {α, β}
= {β, α}. If α is lexical and β phrasal (that is, if β but not α
is of form {ϒ, Ơ}) then form the consideration {a, b} = {a, {ϒ, Ơ}} one might infer that α
is the head and β is the compliment
(COMP).
However, if both are lexical, one must farther specify which the head
is. Similarly, if α = {ϒ, {Ơ, ɳ}} and β is lexical, then either β
is the specifier (SPEC) of ϒ, or α
is the COMP of β, and one must
farther specify which. Chomsky reacts that, “ϒ must therefore at least (and we assume at most) be of the form {Ơ, {α,
β}}, where Ơ identifies the relevant
properties of ϒ; calls Ơ the label of ϒ … If α projects, is the head then ϒ = {α, {α, β}}”
Chomsky maintains that a more complex form of merge is required to generate adjoined
structures – calls this operation ‘pair merge’. But it is an empirical fact
that there is also an asymmetric operation of adjunction, which takes two
objects β, and α and forms the
ordered pair <α, β>, α
adjoined to β. Given the basic properties of adjunction, we might intuitively
think of α as attached to β
on a separate plane, with β retaining
all its properties on the ‘primary plane’ the simple structure. Langendoen
(2001) presents the pair merge of β adjoined to α as P (α, β) = <α, β>
The structure of the coordinate phrase Y and Z in figure (a) and of
the coordinate phrase X, Y and Z in figure (b); in both structures <and, Z> in the head.
Another distribution that might be
dispensed with in the minimalist approach is the distinction between
substitution and adjunction.
In the present framework, two types of
internal pair merges are possible, one of which is adjunction of β to
α where α = <ϒ, Ơ….>
is past of β. Application of
internal head pair merge (adjunction of β
to α, where α is part of β) results in the “readjustment” of structure, as in the
application of “readjustment rules”. For example
in P (<ϒ, Ơ, …>, β/ <ϒ, Ơ, …>) = <<ϒ, Ơ,…>, β/<ϒ, Ơ,
...>>, let β be the structure
in the following figure which is the argument structure of “they thought that you liked them”, and α
= <that, <liked, them, you>>
(so that ϒ = that and Ơ = <liked, them, you>).
However, Szwedek (2010) poses criticism
as the minimalist program reveals the deficiencies such as rejection of
semantics and pragmatics, and disrespect for language data, and Chomsky’s
questionable attitude towards earlier research that has in no way been
explained.
Finally, the minimalist program is a
major contribution in that it lays the groundwork for a new stage in syntactic
theorizing. And so it is not essentially different from previous version of the
theory of generative syntax. The most important fact of minimalism is that it
turns the traditional, top- down approach to investigating universal grammar
(UG). It seeks to approach the problem ‘from bottom up’. This suffices to say
that the field is rapidly changing under the impact of new empirical materials
and theoretical ideas. What looks reasonable today is likely to take a
different form tomorrow. However, minimalism is the research program rather
than a theory.
REFERENCE
Szwedek, A (2010), Stadia Anglica
Posnanensia: International Review of
English Studies, Adam Mickiewcz University.








No comments:
Post a Comment